Real-time Kinetics (RTK)

Centimeter-level accuracy for the transportation of the future

Introduction

Whenever we talk about autonomous vehicles — either terrestrial or aerial — there are few elements more important than precise location.

For C-V2X in particular, being able to provide one’s location with centimeter-level accuracy is crucial for any type of accident prevention algorithm: telling which lane a vehicle is on or exactly how far behind a car is becomes of paramount importance; traditional GNSS (Global Navigation Satellite System) is just not accurate enough.

Strategies

All current strategies for improving GNSS accuracy involve placing a number of fixed-position stations in strategic places (e.g. top of buildings, light poles) which can then measure the GNSS positioning errors and provide these measurements to receivers in the surrounding area, allowing these receivers to make the appropriate corrections in the calculations.

Some of these strategies are:

Differential GPS

Differential GPS uses a fixed-position station located in a known, surveyed position. The station’s position can be also determined by measuring the GPS coordinates over 24 hours or longer and using the average location as the ground truth.

By comparing the measured location from GPS and the known position, the station can determine the error in measurement and provide that information to the receivers.

This approach produces sub-10 meters accuracy depending on the receiver’s distance from the station with a typical error between 1 and 3 meters.

The U.S. Coast Guard provides DGPS services for maritime use, in particular for ships approaching a port; the correction data is broadcast in maritime radiobeacon frequencies.

SBAS (Space Based Augmentation System)

SBAS uses a set of geostationary satellites with known positions that allows fixed-position base stations to calculate GNSS errors.

SBAS allows for sub-2 meters accuracy. There are 4 systems in operation: WAAS (North and Central America), EGNOS (European system), GAGAN (India) and MSAS (Japan).

SSR (Space State Representation)

SSR uses the data collected by fixed-position stations and use them with atmospheric mathematical models to calculate the corrections to be applied to the measured coordinates.

Base stations are placed about 150 km apart and provide sub-10 cm accuracy. Skylark, by Swift Navigation, is one such commercially available service.

RTK (Real-time Kinetics)

RTK measures phase errors in the signal received by the fixed-position base stations to determine the corrections to be applied to the calculated position.

RTK provides sub-3 cm accuracy to receivers within 10 km from the station. This is the system we will explore in this article.

The mathematics of GNSS

The mathematical principle behind GNSS positioning is relatively simple. Here is the basic equation:

Equation 1: LIght-cone equation

The equation has 3 variables — latitude, longitude and altitude — so, in principle, if we know the position of 3 satellites and the time it takes for the signal from each satellite to get to the receiver we can calculate the receiver’s position.

However, there is a catch. The speed of light is ~300,000 km/s; introducing 1 millisecond of error in the time measurement means the distance measurements in the receiver will be off by 300 km.

So things get quite more complicated once errors are introduced to the time measurements. For example:

• Clock biases in both the transmitter and receiver
• The speed of light changes when crossing the ionosphere and troposphere
• Multipath affects the time measurements and therefore distance calculations
• Dilution of precision due to the relative positions of satellites and receiver
• Electronic and radio noise
• Doppler effects in the frequency
• Relativistic effects due to gravity

Some of these errors are known or can be modeled; others cannot. Here is where RTK comes to the rescue, allowing these unknown errors to be eliminated from the measurement for an extremely accurate position calculation.

Pseudorange and point positioning

Before we start, it is important to understand how the GNSS receiver measures the time delay used in equation 1 and calculates its position in the presence of unknown error.

Pseudo-random code

Each satellite in a GNSS constellation provides its information in a radio signal modulated by a pseudo-random code unique to the satellite. The pseudo-random code is a long binary sequence, designed to look like noise. It’s the same principle used in the CDMA cell phone technology.

So, how does the receiver measure the time delay? It generates the same sequence of bits, based on its internal clock, at the same time it would be transmitted by the satellite.

Then it compares the received bits with the locally generated ones and measured the time difference between the two sequences. And that is the time interval it uses in equation 1.

Figure 1: Time delay measurement. Source: Geoffrey Blewitt, Basics of the GPS Technique: Observation Equations

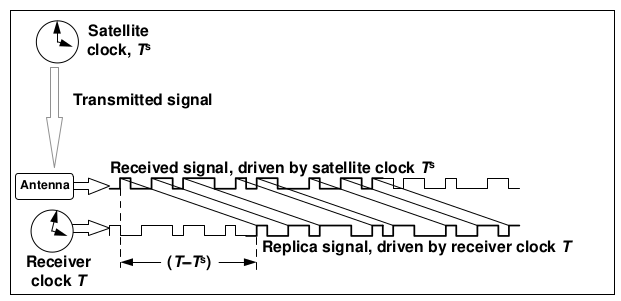
But, this measured time delay is not accurate; it is affected by all the errors mentioned before so let’s see how we mitigate this problem.

Least square method

So what we end up with is a system of nonlinear equations that must be resolved in order to determine the current position.

Depending on the number of visible satellites, this system of equations is over-determined — it has more equations than variables.

The approach to resolve this type of system is to calculate the position (x,y,z) that minimizes the sum of the square of the errors from all satellites; for that the Gauss-Newton algorithm is used.

The algorithm resembles the Newton method to find the roots/minima/maxima of a function and is designed to resolve nonlinear least square equations.

This technique allows a standalone receiver to determine its position with a certain degree of accuracy but it cannot eliminate the errors.

RTK and carrier-phase observation

The core difference between RTK and pseudorange — besides of course the presence of fixed-position base stations — is that it uses, instead of the pseudo-random code, the carrier signal — especifically, the signal’s phase with respect to a locally generated signal — to determine the time delay.

Then, by subtracting the measured phases from the rover and a fixed-position base station, almost all errors are eliminated except the phase’s integer ambiguity.

So let’s start understanding the phase measurements, model for the phase errors and how the integer ambiguity resolution becomes the key for the high-accuracy of RTK.

Measuring distances using phase

Let’s use simple sinusoidal functions to explain how we can measure phase and what is the integer ambiguity.

Consider 2 sinusoidal signals, one sent by a transmitter at some unknown distance from the receiver and one generated locally at the receiver:

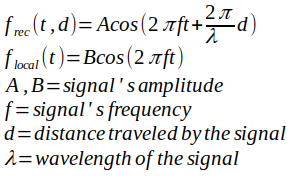
The first equation is for the travelling wave through space, and represents what we see at the receiver. The term depending on the distance is the phase of the travelling signal relative to the receiver.

If we multiply the 2 equations, we obtain a sum of cosines where the second term depends only on the phase, which depends on the distance between transmitter and receiver.

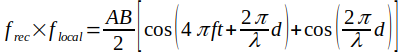
However, the distance d can be written as a function of the signal wavelength; therefore:

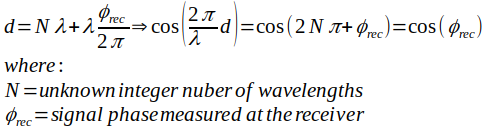
So it’s clear that, by just measuring the phase, we cannot determine the full distance between the transmitter and the receiver since, in reality, we can only measure the small fractional part of the phase difference.

The unknown N represents the integer ambiguity.

Eliminating the errors

As we explained before, RTK relies on fixed-position base stations with well known coordinates.

At these base stations, one can model the signal phase measured for each satellite as (units in meters and seconds):

The clock biases affect the satellite and receiver clock starting point for the GNSS and the reference signals and, consequently, the phase measurement.

The phase equation is the same for the GNSS receiver.

The procedure used to eliminate all errors is called double difference, and it goes like this:

1. Base-station measures the phase for 2 satellites, 1 and 2
2. Base-station sends to the receiver its own known coordinates, the satellites it used and the phases for each one
3. The receiver measures the phases for the same satellites 1 and 2
4. The receiver then performs the double difference operation

Assuming the ionospheric and tropospheric errors are the same for both the base station and the receiver — as long as they are within 10 km of each other— and the noise and multipath errors are small, here is the final equation after the double difference operation:

And voilá, the equation now depends only on resolving the integer ambiguity since the phases are all measured, the distances between stations and satellites are known and the initial, inaccurate distance between the receiver and the satellites can be determined using the usual pseudorange method.

The general algorithm is:

1. Use pseudoranges and calculate the ambiguities as a float numbers — called float mode
2. Find the integer ambiguity around the float values; this is the most complicated part and different methods can be used for this step
3. Calculate the accurate receiver position relative to the base station using the integers determined in step 2 to calculate the position of the receiver relative to the base station

Once integer ambiguity is resolved, RTK goes into fixed mode. That is because the GNSS wavelength is around 20 cm so fractional errors in the phase measurement assure small positioning errors, as opposed to small errors in time measurement, which cause errors in the order of meters.

Now the receiver can keep track of the phase changes — increasing or decreasing — and, when it turns to zero, the receiver increments or decrements N accordingly. In fixed mode it can provide accuracies below 3 cm.

The caveat is that, if the receiver loses the GNSS signal, it has to start over.

The calculations described in this section obviously require the receiver to get data from the base stations. Let’s see how this is done.

RTCM and NTRIP

RTCM stands for Radio Technical Commission for Maritime Services; it is an international non-profit independent organization that defines a number of different protocols for radio communication.

It defines the Differential GNSS (Global Navigation Satellite Systems) Services, currently in version 3 (RTCM 10403.3), which:

(…) defines messages that are used improve the accuracy of location provided by Global Navigation Satellite Systems (GNSS) such as GPS, GLONASS, Galileo, QZSS, and BeiDou (BDS).

The messages defined in this specification can be transmitted to the receiver using different radio technologies; one popular method is using NTRIP (Network Transport of RTCM by Internet Protocol).

NTRIP specifies how to encapsulate correction data in IP packets and deploy it to the receiver, making it a very convenient way to make RTK available to connected vehicles, since they can take advantage of pre-existing cellular connectivity without the need for installing yet another radio in the car.

NTRIP has a relatively simple architecture:

1. Caster: HTTP server that receives the client request for RTCM data, usually using some API that allows the caster to select the most appropriate base station for that client
2. Server: responsible for receiving the correction data from the base stations
3. Client: co-located with the GNSS receiver, responsible for collecting the correction data and providing it to the receiver for processing.

RTK2GO, Swift Navigation’s Skylark and Verizon are providers of NTRIP services, just to name a few.

Conclusion

Precision location is a fundamental technology for many applications. To name a few:

• Land survey
• Autonomous drone flight
• Autonomous cars
• Traffic accident prevention

RTK is a convenient, relatively cheap technology that can provide reliable precise location. RTK boards are relatively affordable, with prices varying around USD 200.00.

Several companies are deploying RTK and SSR services in the US, covering large, highly populated areas.

Many car manufacturers are very interested in supporting RTK as part of their C-V2X offer in their vehicles.

Municipalities and the Department of Transportation are also very interested in C-V2X and, by extension, RTK; in 2010, in the US alone, car crashes cost an estimated $871 billion dollars in economic loss and societal harm (see this report from the U.S Department of Transportation).

Systems like C-V2X with RTK support cost a fraction of that amount to be installed, maintained and operated and can help saving numerous lives.

With C-V2X and RTK I see a bright future for a safer, cheaper and more reliable transportation system.